Content
Algorithm Bellman-Ford
The algorithm Bellman-Ford solves the problems in which there is to find the shortest paths from a source node given with the condition that they contain at most one link
Find the shortest paths with the condition of containing two links maximum
And so on until the maximum number of shortest paths
Where:
- s = source node
- w(i, j) = link cost from node i to node j:
- w(i, i) = 0
- w(i, j) = \infty if the two nodes are not directly connected
- w(i, j) \geq 0 if the two nodes are directly connected
- h = maximum number of links in a path in the current step of the algorithm
- L_h(n) = cost of the path of minimum cost from the node s to the node n with the condition that there is no more than h links
For resolution you can use the Bellman-Ford algorithm method, which consists of applying the following steps:
- Initialization
- Update
Step 1: Initialization
L_0(n) = \infty, \forall n \not= s
L_h(n) = 0, \forall h
Step 2: Update
- For each successive h \geq 0, \forall n \not= s calculate:
L_{h+1}(s)=\min_j{[L_h(j)+w(j, n)]} - Connect n with the node predecessor j of minimum cost
- Remove all connections of n with a node predecessor different obtained in a previous iteration
- The path from s to n terminates with link from j to n
Annotations to the algorithm, Bellman-Ford
For the iteration of step 2 with h'K, and for each target node n, the algorithm compares the potential paths of length K + 1 from s to n with the existing path at the end of the previous iteration
If the shortest path before has a lower cost, it is saved
Otherwise, a new path is defined
Example of algorithm Bellman-Ford
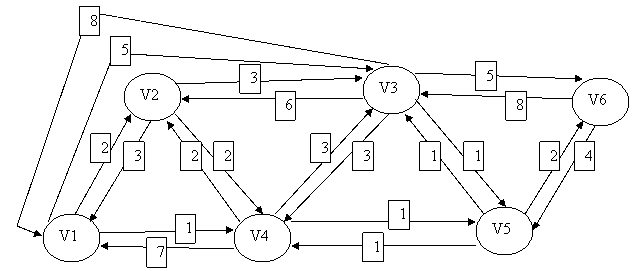
The chart shows the representation of a communication network in which each segment represents the maximum capacity of transfer per unit of time
It is requested to:
To get from node V1 to node V6
| h | L_h(2) | Route | L_h(3) | Route | L_h(4) | Route | L_h(5) | Route | L_h(6) | Route |
| 0 | \infty | – | \infty | – | \infty | – | \infty | – | \infty | – |
| 1 | 2 | 1-2 | 5 | 1-3 | 1 | 1-4 | \infty | – | \infty | – |
| 2 | 2 | 1-2 | 4 | 1-4-3 | 1 | 1-4 | 2 | 1-4-5 | 10 | 1-3-6 |
| 3 | 2 | 1-2 | 3 | 1-4-5-3 | 1 | 1-4 | 2 | 1-4-5 | 4 | 1-4-5-6 |
| 4 | 2 | 1-2 | 3 | 1-4-5-3 | 1 | 1-4 | 2 | 1-4-5 | 4 | 1-4-5-6 |
According to the Bellman-Ford algorithm we will have to follow the V1-V4-V5-V6 nodes, because they are the ones that cause the least cost
