Definition

The complex numbers give a solution to the equation x^2+1=0, how x^2=-1 has as a solution x=\pm{\sqrt{-1}}, which has no real solution

We will use as a solution x=\pm{i}. Where i is the imaginary unit of the complex number

We will call complex number expression z=a+b\cdot{i} (binomic form) where a, b\in{\mathbb{R}}. Being to the real part of the number and b its imaginary part

Are an ordered pair of real numbers (a, b) \in{\mathbb{R} \times \mathbb{R}}

In the event that b=0 then we can consider the number as real, since the actual numbers are a subset of the complex

The set of complex numbers is denoted as \mathbb{C}

Two basic types of operations are defined: addition and multiplication

Graph of a complex

We will draw the graph of a complex

Given a complex number z=a+b\cdot{i}=(a, b) \in \mathbb{R} x \mathbb{R} is an ordered pair of real numbers, represented by the point (a, b) on the XY plane, called complex plane

The dot (a, b) is called the z-complex number

Example of graph of a complex

Given the following complex we want to represent:

z=(-3)+4\cdot{i}

We get the following graph:

Argument

Argument:

The value of the angle \alpha receives the name of argument

For a given complex number, the argument supports an infinite set of values, which differ from each other in 2\cdot{k}\cdot{\pi}; k\in{\mathbb{Z}}

It's called principal value of the argument the one that meets 0\leq\alpha\leq{2}\cdot{\pi}

It can be calculated by:

\alpha=Arg(z)=atan2(b, a)=\begin{cases} \arctan(\frac{b}{a}) & \text{if }a > 0 \\ \arctan(\frac{b}{a}) + \pi & \text{if }b \geq 0, a < 0 \\ \arctan(\frac{b}{a}) - \pi & \text{if }b < 0, a < 0 \\ \frac{\pi}{2} & \text{if }b > 0, a = 0 \\ \frac{-\pi}{2} & \text{if }b < 0, a = 0 \\ \text{Undefined} & \text{if }b = 0, a = 0 \end{cases}

This result is obtained in radians and sometimes it will be useful to convert it to degrees:

\alpha=\frac{atan2(b, a)\cdot{360}}{2\cdot\pi}

You can also use the following table that expresses trigonometric reasons:

	>rad	>\sin \alpha	>\cos \alpha	\tan \alpha = \frac{\sin \alpha}{\cos \alpha}
>0^{\circ}	>0	>0	>1	>0
>30^{\circ}	>\frac{\pi}{6}	>\frac{1}{2}	>\frac{\sqrt{3}}{2}	>\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}
>45^{\circ}	>\frac{\pi}{4}	>\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}	>\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}	>1
>60^{\circ}	>\frac{\pi}{3}	>\frac{\sqrt{3}}{2}	>\frac{1}{2}	>\sqrt{3}
>90^{\circ}	>\frac{\pi}{2}	>1	>0	>\text{Undefined}
>180^{\circ}	>\pi	>0	>-1	>0
>270^{\circ}	>\frac{3\cdot\pi}{2}	>-1	>0	>\text{Undefined}

Example of argument

\begin{cases}z=(-3)+4\cdot{i} \\ \alpha=atan2(4, -3)=2.2143\text{ radians}\end{cases}

\alpha=\frac{atan2(4, -3)\cdot{360}}{2\cdot\pi}=\frac{2.2143\cdot{360}}{2\cdot\pi}=\frac{797.148}{2\cdot\pi}=126.8701^{\circ}\approx\frac{2\cdot\pi}{3}

So we have to:

\alpha\approx\frac{2\cdot\pi}{3}

Module

Module and its properties

Given a complex number z=a+b\cdot{i}, is defined as module, or absolute value to the expression:

r=\|a+b\cdot{i}\|=\sqrt{a^2+b^2}

Given z_1, z_2, \cdots, z_n \in{\mathbb{C}} it is fulfilled that:

1. \|z_1\cdot{z_2}\cdot\text{ }\cdots\text{ }\cdot{z_n}\|=\|z_1\|\cdot\|z_2\|\cdot\text{ }\cdots\text{ }\cdot\|z_n\|
2. \|\frac{z_1}{z_2}\|=\frac{\|z_1\|}{\|z_2\|}\text{ con }\|z_2\|\not{=}0
3. \|z_1+z_2\|\leq\|z_1\|+\|z_2\|
4. \|z_1+z_2+\text{ }\cdots\text{ }+z_n\|\leq\|z_1\|+\|z_2\|+\text{ }\cdots\text{ }+\|z_n\|

Example of module

z=(-3)+4\cdot{i}

\|z\|=\|(-3)+4\cdot{i}\|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5

So we have to:

\|z\|=5

Forms of a complex number

Form of a complex number:

• polar
• trigonometric
• exponential

Polar

Given the point (a, b) I sharpen the complex number z=a+b\cdot{i} whose module is r and its argument is \alpha, its representation in polar shape it is z=r_\alpha

Example of a polar

z=(-3)+4\cdot{i}

\|z\|=\|(-3)+4\cdot{i}\|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5

\alpha=\frac{atan2(4, -3)\cdot{360}}{2\cdot\pi}=\frac{2.2143\cdot{360}}{2\cdot\pi}=\frac{797.148}{2\cdot\pi}=126.8701^{\circ}\approx\frac{2\cdot\pi}{3}

So we have to:

z=5_{\frac{2\cdot\pi}{3}}

Trigonometric

It can also be represented in trigonometric shape where

\begin{cases}a=r\cdot\cos{\alpha} \\ b=r\cdot\sin{\alpha} \end{cases}

with what we have

z=a+b\cdot{i}=r\cdot(\cos{\alpha}+\sin{\alpha}\cdot{i})

Example of a trigonometric

z=(-3)+4\cdot{i}

\|z\|=\|(-3)+4\cdot{i}\|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5

\alpha=\frac{atan2(4, -3)\cdot{360}}{2\cdot\pi}=\frac{2.2143\cdot{360}}{2\cdot\pi}=\frac{797.148}{2\cdot\pi}=126.8701^{\circ}\approx\frac{2\cdot\pi}{3}

So we have to:

z=a+b\cdot{i}=5\cdot(\cos(\frac{2\cdot\pi}{3})+\sin(\frac{2\cdot\pi}{3})\cdot{i})

Exponential

It can also be represented in exponentially shape where

\begin{cases}\sin\alpha=\frac{e^{\alpha\cdot{i}}-e^{(-\alpha)\cdot{i}}}{2\cdot{i}} \\ \cos\alpha=\frac{e^{\alpha\cdot{i}}+e^{(-\alpha)\cdot{i}}}{2}\end{cases}

with what we have to

z=a+b\cdot{i}=r\cdot(\cos{\alpha}+\sin{\alpha}\cdot{i})=r\cdot{e^{\alpha\cdot{i}}}

Example of exponential

z=(-3)+4\cdot{i}

\|z\|=\|(-3)+4\cdot{i}\|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5

\alpha=\frac{atan2(4, -3)\cdot{360}}{2\cdot\pi}=\frac{2.2143\cdot{360}}{2\cdot\pi}=\frac{797.148}{2\cdot\pi}=126.8701^{\circ}\approx\frac{2\cdot\pi}{3}

So we have to:

z=a+b\cdot{i}=5\cdot{e^{\frac{2\cdot\pi}{3}\cdot{i}}}

Moivre formula

Moivre Formula:

The power n-th entry of a complex number r_\alpha it is another complex module r^n and argument n times the argument of the first

In consequence, we have that

z^n={(r_\alpha)}^n=\overbrace{r_\alpha \cdots r_\alpha}^{n\;\rm times}={(r^n)}_{n\cdot\alpha}

Example of Moivre's formula

\tiny\begin{cases}z^4={((-3)+4\cdot{i})}^4 \\ \|z\|=\|-3+4\cdot{i}\|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5 \\ \alpha=\frac{atan2(4, -3)\cdot{360}}{2\cdot\pi}=\frac{2.2143\cdot{360}}{2\cdot\pi}=\frac{797.148}{2\cdot\pi}=126.8701^{\circ}\approx\frac{2\cdot\pi}{3} \end{cases}

z^4={(5_{\frac{2\cdot\pi}{3}})}^4=(5^4)_{4\cdot{\frac{2\cdot\pi}{3}}}=625_{\frac{8\cdot\pi}{3}}

So we have to:

z^4={(r_\alpha)}^n=625_{\frac{8\cdot\pi}{3}}

Roots n-ésimas of a complex number

Given a complex number z=r_{\alpha}\text{ si }w=s_{\beta} it is a root n-th we have that

\begin{cases} z={(s_\beta)}^n={(r^n)}_{n\cdot\beta}=r_{\alpha} \\ s^n=r \\ n\cdot{\beta}=\alpha+2\cdot{k}\cdot\pi \\ s=\sqrt[n]{r} \\ \beta=\frac{(\alpha+2\cdot{k}\cdot\pi)}{n} \\ z_k=\sqrt[n]{r}\cdot{e}^{{\frac{(\alpha+2\cdot{k}\cdot\pi)}{n}}\cdot{i}} \end{cases}

with k=0,1,2,\cdots,(n-1) since for k=n gives the same value as for k=0

There are thus n roots of the n-ésimas different if z\not=0

Example of cube roots

\begin{cases} z^3+2=0\rightarrow{z^3=-2}\rightarrow{z=(-2)^{1/3}} \\ \|z\|=\|(-2)+0\cdot{i}\|=\sqrt{(-2)^2+0^2}=\sqrt{4+0}=\sqrt{4}=2 \\ \alpha=\frac{atan2(0, -2)\cdot{360}}{2\cdot\pi}=\frac{\pi\cdot{360}}{2\cdot\pi}=\frac{360}{2}=180^{\circ}\approx\pi \\ \beta=\frac{\pi+2\cdot{k}\cdot{\pi}}{3} \end{cases}

\begin{cases} z_1={\sqrt[3]{2}} \cdot{e}^{{\frac{\pi+2\cdot{0}\cdot{\pi}}{3}}\cdot{i}}={\sqrt[3]{2}}\cdot{e}^{{\frac{\pi}{3}}\cdot{i}} \\ z_2={\sqrt[3]{2}} \cdot{e}^{{\frac{\pi+2\cdot{1}\cdot{\pi}}{3}}\cdot{i}}={\sqrt[3]{2}}\cdot{e}^{{\frac{\pi+2\cdot\pi}{3}}\cdot{i}}={\sqrt[3]{2}}\cdot{e}^{{\frac{3\cdot\pi}{3}}\cdot{i}}={\sqrt[3]{2}}\cdot{e}^{\pi\cdot{i}} \\ z_3={\sqrt[3]{2}} \cdot{e}^{{\frac{\pi+2\cdot{2}\cdot{\pi}}{3}}\cdot{i}}={\sqrt[3]{2}}\cdot{e}^{{\frac{\pi+4\cdot\pi}{3}}\cdot{i}}={\sqrt[3]{2}}\cdot{e}^{{\frac{5\cdot\pi}{3}}\cdot{i}} \end{cases}

So we have to:

z^3+2=0\rightarrow\begin{cases} z_1={\sqrt[3]{2}}\cdot{e}^{{\frac{\pi}{3}}\cdot{i}} \\ z_2={\sqrt[3]{2}}\cdot{e}^{\pi\cdot{i}} \\ z_3={\sqrt[3]{2}}\cdot{e}^{{\frac{5\cdot\pi}{3}}\cdot{i}} \end{cases}

Operations of complex numbers

The operations of the complex z_1, z_2, z_3 \in \mathbb{C}

\begin{cases}z_1=a+b\cdot{i} \\ z_2=c+d\cdot{i} \\ z_3=e+f\cdot{i} \end{cases}

Operation sum

To define the sum you have to comply with the following properties

Properties of the sum

1. z_1+z_2 \in{\mathbb{C}}
2. z_1+(z_2+z_3)=(z_1+z_2)+z_3
3. \exists\text{ }0 \in \mathbb{C} | z_1+0=0+z_1=z_1
4. \exists\text{ }(-z_1) \in \mathbb{C} | z_1+(-z_1)=(-z_1)+z_1=0
5. z_1+z_2=z_2+z_1

As meets the above properties, the pair (C, +) has structure of grupo abeliano

Example of sum

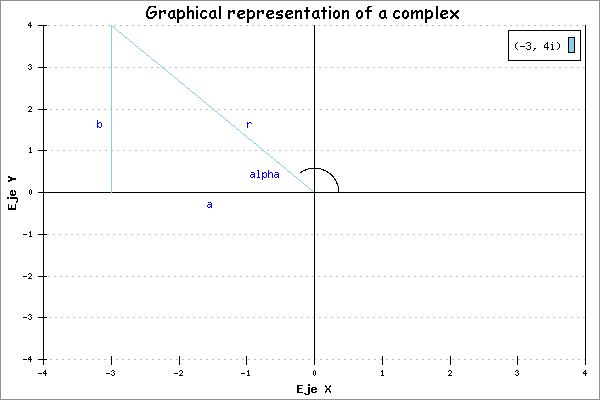
\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1+z_2 \end{cases}

z=((-3)+4\cdot{i})+(5-2\cdot{i})=((-3)+5)+(4-2)\cdot{i}=2+2\cdot{i}

So we have to:

z=z_1+z_2=2+2\cdot{i}

Operation subtraction

Subtraction is a special case of the sum, to realize it you only have to use the sum of the opposite of its real parts and the sum of the opposites of the imaginary parts

Example of subtraction

\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1-z_2 \end{cases}

z=((-3)+4\cdot{i})-(5-2\cdot{i})=((-3)-5)+(4+2)\cdot{i}=(-8)+6\cdot{i}

So we have to:

z=z_1-z_2=(-8)+6\cdot{i}

Operation multiplication

To define multiplication we have to comply with the following properties

Properties of multiplication

1. z_1\cdot{z_2} \in{\mathbb{C}}
2. z_1\cdot(z_2\cdot{z_3})=(z_1\cdot{z_2})\cdot{z_3}
3. \exists\text{ }1 \in \mathbb{C} | z_1\cdot{1}=1\cdot{z_1}=z_1
4. \forall\text{ }(z_1) \in \mathbb{C} (z_1\ne{0}), \exists\text{ }{z_1}^-1 \in \mathbb{C} | z_1\cdot{z_1}^-1={z_1}^-1\cdot{z_1}=1
5. z_1\cdot{z_2}=z_2\cdot{z_1}

As meets the above properties, the pair (\mathbb{C}-\{0\}, \cdot) has structure of grupo abeliano

Example of multiplication

\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1\cdot z_2 \end{cases}

z=((-3)+4\cdot{i})\cdot(5-2\cdot{i})=((-3)\cdot{5})+((-3)\cdot(-2)\cdot{i}))+(4\cdot{i}\cdot{5})+(4\cdot{i}+(-2)\cdot{i})=(-15)+6\cdot{i}+20\cdot{i}-8\cdot{i^2}=(-15)+26\cdot{i}-8\cdot{i^2}=(-15)+8+26\cdot{i}=(-7)+26\cdot{i}

In the case of obtaining a value of an imaginary square (i^2), we will take that value as your real opposite. In the example we appeared (-8)\cdot{i}, we'll take 8 as the actual number that will add to your real part

So we have to:

z=z_1\cdot{z_2}=(-7)+26\cdot{i}

Operation division

Division is a special case of multiplication, to make it only multiply the numerator and denominator by the conjugate of the denominator

The conjugated is obtained by changing the sign of the imaginary part of the denominator

Example of division

\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z={z_1 \over z_2} \end{cases}

z={((-3)+4\cdot{i})\over(5-2\cdot{i})}={((-3)+4\cdot{i})\over(5-2\cdot{i})}\cdot{(5+2\cdot{i})\over(5+2\cdot{i})}=
{(((-3)\cdot{5})+((-3)\cdot{2}\cdot{i})+(4\cdot{i}\cdot{5})+(4\cdot{i}\cdot{2}\cdot{i}))\over((5\cdot{5})+(5\cdot{2}\cdot{i})+((-2)\cdot{i}\cdot{5})+((-2)\cdot{i}\cdot{2}\cdot{i}))}=
{(-15)+(-6)\cdot{i}+20\cdot{i}+(8\cdot{i^2})\over{25}+10\cdot{i}+(-10)\cdot{i}+(-4)\cdot{i^2}}={(-15)+14\cdot{i}+(8\cdot{i^2})\over{25}+(-4)\cdot{i^2}}=
{(-15)-8+14\cdot{i}\over{25}+4}={(-23)+14\cdot{i}\over{29}}={(-23)\over{29}}+{14\cdot{i}\over{29}}

So we have to:

z={z_1 \over z_2}={(-23)\over{29}}+{14\cdot{i}\over{29}}

Operation sum and product

In addition to sum and product share the following property

Property of the sum and the product

6. z_1\cdot(z_2+z_3)=z_1\cdot{z_2}+z_1\cdot{z_3}

As the previous property complies with, the terna (\mathbb{C}, +, \cdot) has structure of body-commutative

Example of sum and multiplication

\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1\cdot(z_2+z_3) \end{cases}

z=((-3)+4\cdot{i})\cdot((5-2\cdot{i})+(8+3\cdot{i}))=((-3)+4\cdot{i})\cdot(5-2\cdot{i}))+((-3)+4\cdot{i})\cdot(8+3\cdot{i}))=((-3)\cdot{5})+((-3)\cdot(-2)\cdot{i})+(4\cdot{i}\cdot{5})+(4\cdot{i}+(-2)\cdot{i})+((-3)\cdot{8})+((-3)\cdot{3}\cdot{i})+(4\cdot{i}\cdot{8})+(4\cdot{i}\cdot{3}\cdot{i})=((-15)+6\cdot{i}+20\cdot{i}-8\cdot{i^2})+((-24)-9\cdot{i}+32\cdot{i}+12\cdot{i^2})=(-15)-24+6\cdot{i}+20\cdot{i}-9\cdot{i}+32\cdot{i}-8\cdot{i^2}+12\cdot{i^2}=(-39)+49\cdot{i}+4\cdot{i^2}=(-39)-4+49\cdot{i}=(-43)+49\cdot{i}

So we have to:

z=z_1\cdot(z_2+z_3)=(-43)+49\cdot{i}