Content
Algorithm Dijkstra
The Dijkstra algorithm solves the problems in which the shortest paths between a given source node and all other nodes need to be found, developing the paths in increasing order of length
Where:
- N = set of nodes in the network
- s = source node
- T = list or set of nodes added to, or incorporated by the algorithm
- w(i, j) = link cost from node i to node j:
- w(i, i) = 0
- w(i, j) = \infty if the two nodes are not directly connected
- w(i, j) \geq 0 if the two nodes are directly connected
- L_h(n) = cost, of course, obtained by the algorithm for the path of minimum cost from node s to node n
For resolution you can use the Dijkstra algorithm method, which consists of applying the following steps:
- Initialization
- Getting the next node
- Update the paths of minimum cost
Step 1: Initialization
T = {s} the built-in node set only consists of the source node
L(n) = w(s, n), \forall n \not= s
The initial cost of the routes to the neighboring nodes is associated to the links
Step 2: Getting the next node
- Looking to the neighbouring node that is not in T with the path of least cost
- It incorporates the node in T
- It incorporates the link from that node to a node of T that is part of the way
Step 3: Updating the Minimum Cost Roads
The following formula applies:
L(n) = \min{[L(n), L(x) + w(x, n)]}, \forall n \not\in T
The algorithm concludes when all nodes have been added to T
Annotations to the algorithm Dijkstra
In the end, the L(x) value associated with each x node is the cost (length) of the minimum cost path from s to x
T defines the path of minimum cost from s to any other node
Each iteration of steps 2 and 3 incorporates a new node to T that defines the minimum cost path from s to that node, traversing that path only nodes included in T
Example of the algorithm Dijkstra
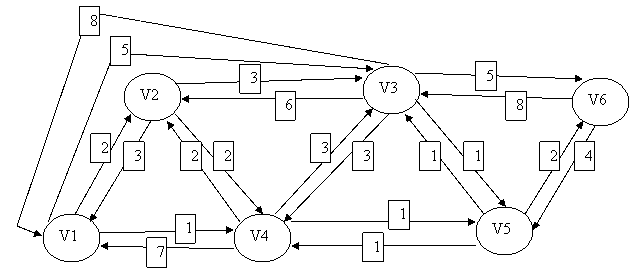
The chart shows the representation of a communication network in which each segment represents the maximum capacity of transfer per unit of time
It is requested to:
To get from node V1 to node V6
| i | T | L_h(2) | Route | L_h(3) | Route | L_h(4) | Route | L_h(5) | Route | L_h(6) | Route |
| 1 | {1} | 2 | 1-2 | 5 | 1-3 | 1 | 1-4 | \infty | – | \infty | – |
| 2 | {1, 4} | 2 | 1-2 | 4 | 1-4-3 | 1 | 1-4 | 2 | 1-4-5 | \infty | – |
| 3 | {1, 2, 4} | 2 | 1-2 | 4 | 1-4-3 | 1 | 1-4 | 2 | 1-4-5 | \infty | – |
| 4 | {1, 2, 4, 5} | 2 | 1-2 | 3 | 1-4-5-3 | 1 | 1-4 | 2 | 1-4-5 | 4 | 1-4-5–6 |
| 5 | {1, 2, 3, 4, 5} | 2 | 1-2 | 3 | 1-4-5-3 | 1 | 1-4 | 2 | 1-4-5 | 4 | 1-4-5–6 |
| 6 | {1, 2, 3, 4, 5, 6} | 2 | 1-2 | 3 | 1-4-5-3 | 1 | 1-4 | 2 | 1-4-5 | 4 | 1-4-5–6 |
According to the Dijkstra algorithm we will have to follow the V1-V4-V5-V6 nodes, because they are the ones that cause the least cost
