Algoritmo Dijkstra

El algoritmo Dijkstra resuelve los problemas en los que hay que encontrar las rutas más cortas entre un nodo origen dado y todos los demás nodos, desarrollando los caminos en orden creciente de longitud

Donde:

• N = conjunto de nodos en la red
• s = nodo origen
• T = lista o conjunto de nodos añadidos o incorporados por el algoritmo
• w(i, j) = coste del enlace desde el nodo i al nodo j:
  • w(i, i) = 0
  • w(i, j) = \infty si los dos nodos no se encuentran directamente conectados
  • w(i, j) \geq 0 si los dos nodos están directamente conectados
• L_h(n) = coste en curso obtenido por el algoritmo para el camino de mínimo coste del nodo s al nodo n

Para su resolución se puede emplear el método del algoritmo Dijkstra, que consiste en aplicar los siguientes pasos:

1. Inicialización
2. Obtención del siguiente nodo
3. Actualización de los caminos de mínimo coste

Paso 1: Inicialización

T = {s} el conjunto de nodos incorporado sólo consta del nodo origen

L(n) = w(s, n), \forall n \not= s

El coste inicial de las rutas a los nodos vecinos es el asociado a los enlaces

Paso 2: Obtención del siguiente nodo

1. Se busca el nodo vecino que no esté en T con el camino de menor coste
2. Se incorpora el nodo en T
3. Se incorpora el enlace desde ese nodo hasta un nodo de T que forma parte del camino

Paso 3: Actualización de los caminos de mínimo coste

Se aplica la siguiente fórmula:

L(n) = \min{[L(n), L(x) + w(x, n)]}, \forall n \not\in T

El algoritmo concluye cuando todos los nodos han sido añadidos a T

Anotaciones al algoritmo Dijkstra

Al final, el valor L(x) asociado a cada nodo x es el coste (longitud) de la ruta de mínimo coste de s a x

T define la ruta de mínimo coste desde s hasta cualquier otro nodo

Cada iteración de los pasos 2 y 3 incorpora un nuevo nodo a T que define el camino de mínimo coste desde s hasta ese nodo, atravesando dicha ruta sólo nodos incluidos en T

Ejemplo del algoritmo Dijkstra

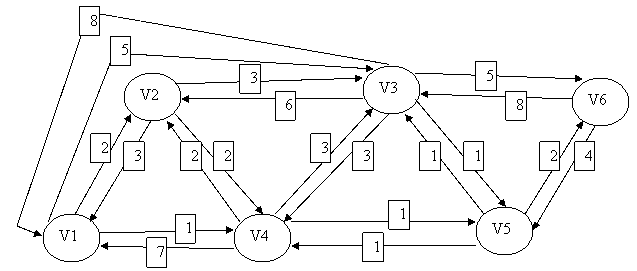
En el gráfico se muestra la representación de una red de comunicación en la que en cada tramo representa la capacidad máxima de transferencia por unidad de tiempo

Se pide:

Llegar del nodo V1 al nodo V6

i	T	L_h(2)	Ruta	L_h(3)	Ruta	L_h(4)	Ruta	L_h(5)	Ruta	L_h(6)	Ruta
1	{1}	2	1-2	5	1-3	1	1-4	\infty	–	\infty	–
2	{1, 4}	2	1-2	4	1-4-3	1	1-4	2	1-4-5	\infty	–
3	{1, 2, 4}	2	1-2	4	1-4-3	1	1-4	2	1-4-5	\infty	–
4	{1, 2, 4, 5}	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5–6
5	{1, 2, 3, 4, 5}	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5–6
6	{1, 2, 3, 4, 5, 6}	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5–6

Según el algoritmo Dijkstra deberemos seguir los nodos V1-V4-V5-V6, por ser los que menor coste nos ocasionan