Algoritmo Bellman-Ford

El algoritmo Bellman-Ford resuelve los problemas en los que hay que encontrar los caminos más cortos desde un nodo origen dado con la condición de que éstos contengan a lo sumo un enlace

Encontrar los caminos más cortos con la condición de que contengan dos enlaces como máximo

Y así sucesivamente hasta el número máximo de caminos más cortos

Donde:

• s = nodo origen
• w(i, j) = coste del enlace desde el nodo i al nodo j:
  • w(i, i) = 0
  • w(i, j) = \infty si los dos nodos no se encuentran directamente conectados
  • w(i, j) \geq 0 si los dos nodos están directamente conectados
• h = número máximo de enlaces en un camino en el paso actual del algoritmo
• L_h(n) = coste del camino de mínimo coste desde el nodo s hasta el nodo n con la condición de que no haya más de h enlaces

Para su resolución se puede emplear el método del algoritmo Bellman-Ford, que consiste en aplicar los siguientes pasos:

1. Inicialización
2. Actualización

Paso 1: Inicialización

L_0(n) = \infty, \forall n \not= s
L_h(n) = 0, \forall h

Paso 2: Actualización

1. Para cada sucesivo h \geq 0, \forall n \not= s calcular:
   L_{h+1}(s)=\min_j{[L_h(j)+w(j, n)]}
2. Conectar n con el nodo predecesor j de mínimo coste
3. Eliminar todas las conexiones de n con un nodo predecesor diferente obtenido en una iteración anterior
4. El camino de s a n finaliza con el enlace de j a n

Anotaciones al algoritmo Bellman-Ford

Para la iteración del paso 2 con h = K, y para cada nodo de destino n, el algoritmo compara las rutas potenciales de longitud K + 1 desde s hasta n con el camino existente al final de la iteración anterior

Si el camino más corto previo tiene un coste inferior, se guarda

En caso contrario, se define un nuevo camino

Ejemplo del algoritmo Bellman-Ford

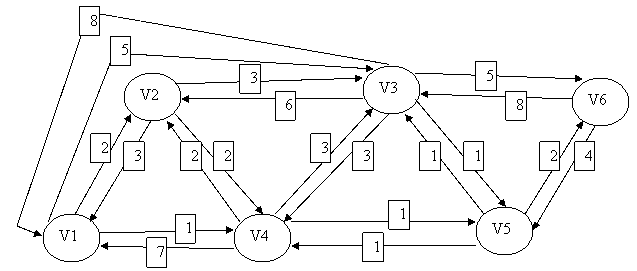
En el gráfico se muestra la representación de una red de comunicación en la que en cada tramo representa la capacidad máxima de transferencia por unidad de tiempo

Se pide:

Llegar del nodo V1 al nodo V6

h	L_h(2)	Ruta	L_h(3)	Ruta	L_h(4)	Ruta	L_h(5)	Ruta	L_h(6)	Ruta
0	\infty	–	\infty	–	\infty	–	\infty	–	\infty	–
1	2	1-2	5	1-3	1	1-4	\infty	–	\infty	–
2	2	1-2	4	1-4-3	1	1-4	2	1-4-5	10	1-3-6
3	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5-6
4	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5-6

Según el algoritmo Bellman-Ford deberemos seguir los nodos V1-V4-V5-V6, por ser los que menor coste nos ocasionan