Contenidos
Método Simplex
Se puede emplear el método Simplex para la resolución de problemas consistentes en maximizar o minimizar una función lineal de variables, con restricciones en forma de igualdades o desigualdades de funciones lineales de dichas variables, y con todas las variables acotadas superior o inferiormente
Aplicando los siguientes pasos:
- Planteamiento del problema en forma estándar
- Aplicación del algoritmo del Simplex
- Determinación de la solución obtenida
Paso 1: Planteamiento del problema en forma estándar
- Se debe poner la función como «minimizar»
- Si es necesario, se realizan cambios de variable para que todas las variables tengan 0 como cota inferior (X_i\geq 0, \forall i)
- Las restricciones se ponen con el término constante positivo
- Se convierten las desigualdades de las restricciones en igualdades añadiendo las variables de holgura
- Se añaden variables artificiales en las restricciones que no tienen una variable en la base, y se añade a la función objetivo la suma de esas variables artificiales multiplicadas por M (que se considera con un valor altísimo)
- Se rellena la tabla para aplicar el algoritmo del Simplex. Su estructura es la siguiente:
X_1 \cdots X_n X básicas a b c-z X_1 \cdots X_n es la alineación de las variables originales, las variables de holgura y las variables artificiales
a son los términos de dichas variables en las restricciones
b son los elementos constantes de dichas restricciones (al otro lado de las variables en las igualdades)
c - z son los costes marginales, en los que c son los coeficientes de la función objetivo, y z_i=c_{b_1}\cdot a_{1 j}+\cdots+c_{b_m}\cdot a_{m i}, siendo m el número de restricciones (de elementos en la base), y donde c_{b_j} representa el coeficiente de la función objetivo correspondiente a la variable j-ésima de las que componen la base. Notar que c - z = 0 siempre para las variables de la base
Paso 2: Aplicación del algoritmo del Simplex
- Elección de la columna de pivote
Se busca el menor elemento de la fila c - z, c\cdot k - z\cdot k de entre los que son negativos y tienen algún elemento positivo en la columna a_k. Si no hay ninguno se termina el algoritmo - Elección de la fila de pivote
Entre los elementos positivos de a_k se busca el que tenga mínimo coeficiente: \frac{b_i}{a_{i k}}, lo llamaremos a_{r k}, y ése será el elemento sobre el que pivotaremos. Si hay varios con el mismo coeficiente se escoge uno cualquiera - Eliminación gaussiana
Se pivota sobre a_{r k}, es decir, se convierte a_k en un vector de la base canónica. Para ello primero se dividen todos los términos de la fila r de a entre a_{r k}, con lo que el nuevo a_{r k} tendrá valor 1 (al dividirse entre sí mismo). Después se anulan los demás elementos de a_k mediante eliminación gaussiana (a cada fila i, con i \not= r, se le suma la nueva fila r multiplicada por X_k). Con ello la variable -a_{i k} habrá entrado en la base (y estará situada en la fila r) - Repetir
Hasta que (c_j - z_j\geq 0, \forall j) \cup (a_k < 0, \forall k\longrightarrow c_k - z_k < 0)
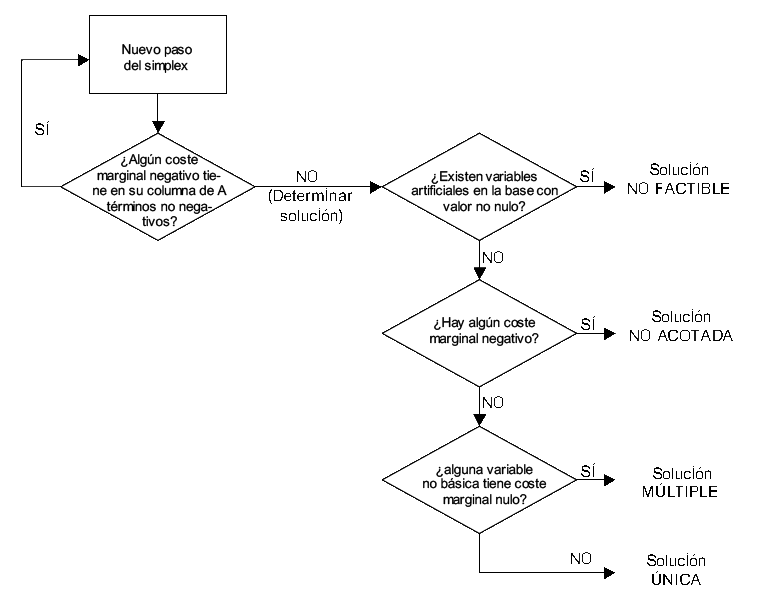
Paso 3: Determinación de la solución obtenida
Si el problema tiene variables artificiales y alguna de ellas presenta valor distinto de cero en la solución final, entonces el problema planteado no tiene solución (no es factible). En caso contrario pasar a los casos siguientes:
- Si (c_j - z_j\geq 0, \forall j) \cap (c_k - z_ k > 0) para las variables no básicas entonces tenemos solución única
- Si (c_j - z_j\geq 0, \forall j) \cap (c_k - z_k = 0) para alguna variable no básica entonces tenemos solución múltiple
- Si \exists (c_k - z_k < 0) (todos ellos han de cumplir que a_k < 0) entonces tenemos una solución no acotada
Ejemplo de problema de Método Simplex
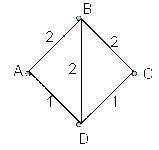
En el gráfico se muestra la representación de una red de comunicación en la que en cada tramo representa la capacidad máxima de transferencia por unidad de tiempo
Se pide:
- Plantea un PPL (problema de programación lineal) cuya solución nos dé la máxima capacidad de transferencia entre A y B y entre C y D (la suma de ambas)
- Resolver el PPL (problema de programación lineal), indicando el tipo de solución que es, su valor, si existe solución, y explicarla
Parte a)
Entre A y B hay 3 caminos que son:
\begin{cases} X_1 \text{ por el camino }A-B \\ X_2 \text{ por el camino }A-D-B \\ X_3 \text{ por el camino }A-D-C-B \end{cases}
Entre C y D hay 3 caminos que son:
\begin{cases} X_4 \text{ por el camino }C-B-A-D \\ X_5 \text{ por el camino }C-B-D \\ X_6 \text{ por el camino }C-D \end{cases}
Por tanto la función a optimizar es:
(X_1+X_2+X_3)+(X_4+X_5+X_6)
Con las restricciones:
\begin{cases} X_1+X_4 \leq 2 \\ X_2+X_3+X_4 \leq 1 \\ X_3+X_4+X_5 \leq 2 \\ X_2+X_5 \leq 2 \\ X_3+X_6 \leq 1 \end{cases}
Con X_1, X_2, X_3, X_4, X_5, X_6 > 0
Parte b)
Maximizar (X_1+X_2+X_3)+(X_4+X_5+X_6)
Minimizar (-X_1-X_2-X_3)+(-X_4-X_5-X_6)
\begin{cases} X_1+X_4+h_1 = 2 \\ X_2+X_3+X_4+h_2 = 1 \\ X_3+X_4+X_5+h_3 = 2 \\ X_2+X_5+h_4 = 2 \\ X_3+X_6+h_5 = 1 \end{cases}
Valores c - z:
columna \tiny X_1 = -1 - ( (-1) \cdot 1 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny X_2 = -1 - ( (-1) \cdot 0 + 0 \cdot 1 + 0 \cdot 0 + 0 \cdot 1 + (-1) \cdot 0 ) = -1
columna \tiny X_3 = -1 - ( (-1) \cdot 0 + 0 \cdot 1 + 0 \cdot 1 + 0 \cdot 0 + (-1) \cdot 1 ) = 0
columna \tiny X_4 = -1 - ( (-1) \cdot 1 + 0 \cdot 1 + 0 \cdot 1 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny X_5 = -1 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 1 + 0 \cdot 1 + (-1) \cdot 0 ) = -1
columna \tiny X_6 = -1 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 1 ) = 0
columna \tiny h_1 = 0 - ( (-1) \cdot 1 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 0 ) = 1
columna \tiny h_2 = 0 - ( (-1) \cdot 0 + 0 \cdot 1+ 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny h3 = 0 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 1 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny h4 = 0 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 1 + (-1) \cdot 0 ) = 0
columna \tiny h5 = 0 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 1 ) = 1
\tiny{\begin{pmatrix}& -1\hspace{1 mm} X_1& -1\hspace{1 mm} X_2& -1\hspace{1 mm} X_3& -1\hspace{1 mm} X_4& -1\hspace{1 mm} X_5& -1\hspace{1 mm} X_6& 0\hspace{1 mm} h_1& 0\hspace{1 mm} h_2& 0\hspace{1 mm} h_3& 0\hspace{1 mm} h_4& 0\hspace{1 mm} h_5& \cr -1\hspace{1 mm} X_1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 2 \cr 0\hspace{1 mm} h_2& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 0& 1 \cr 0\hspace{1 mm} h_3& 0& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 2 \cr 0\hspace{1 mm} h_4& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 0& 2 \cr -1\hspace{1 mm} X_6& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1 \cr & 0& -1& 0& 0& -1& 0& 1& 0& 0& 0& 1&\end{pmatrix}}
Elegimos como pivote la fila 2, columna 2. Por tanto en este caso \frac{b_i}{a_{i k}} será \frac{1}{1}=1
\tiny{\begin{pmatrix}& -1\hspace{1 mm} X_1& -1\hspace{1 mm} X_2& -1\hspace{1 mm} X_3& -1\hspace{1 mm} X_4& -1\hspace{1 mm} X_5& -1\hspace{1 mm} X_6& 0\hspace{1 mm} h_1& 0\hspace{1 mm} h_2& 0\hspace{1 mm} h_3& 0\hspace{1 mm} h_4& 0\hspace{1 mm} h_5& \cr -1\hspace{1 mm} X_1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 2 \cr 0\hspace{1 mm} X_2& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 0& 1 \cr 0\hspace{1 mm} h_3& 0& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 2 \cr 0\hspace{1 mm} h_4& 0& 0& -1& -1& 1& 0& 0& -1& 0& 1& 0& 1 \cr -1\hspace{1 mm} X_6& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1 \cr & 0& 0& 1& 1& -1& 0& 1& 1& 0& 0& -1& 1\end{pmatrix}}
Elegimos como pivote la fila 4, columna 5. Por tanto en este caso \frac{b_i}{a_{i k}} será \frac{1}{1}=1
\tiny{\begin{pmatrix}& -1\hspace{1 mm} X_1& -1\hspace{1 mm} X_2& -1\hspace{1 mm} X_3& -1\hspace{1 mm} X_4& -1\hspace{1 mm} X_5& -1\hspace{1 mm} X_6& 0\hspace{1 mm} h_1& 0\hspace{1 mm} h_2& 0\hspace{1 mm} h_3& 0\hspace{1 mm} h_4& 0\hspace{1 mm} h_5& \cr -1\hspace{1 mm} X_1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 2 \cr 0\hspace{1 mm} h_2& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 0& 1 \cr 0\hspace{1 mm} h_3& 0& 0& 2& 2& 0& 0& 0& 1& 1& -1& 0& 1 \cr 0\hspace{1 mm} X_5& 0& 0& -1& -1& 1& 0& 0& -1& 0& 1& 0& 1 \cr -1\hspace{1 mm} X_6& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1 \cr & 0& 0& 0& 0& 0& 0& 1& 0& 0& 1& -1& 2\end{pmatrix}}
Como no hay más valores negativos en los c – z, c_k - z_k que podamos pivotar, cesamos el algoritmo y obtenemos el siguiente resultado:
\begin{cases} X_1 = 2 \\ X_2 = 1 \\ X_5 = 1 \\ X_6 = 1 \end{cases}
Por tanto, tenemos que X_3 = 0 y X_4 = 0 para que se cumplan las restricciones. Por lo que tenemos que una posible solución a nuestro problema es:
(X_1+X_2+X_3)+(X_4+X_5+X_6) = 5
La solución es múltiple, por tanto, esta solución no es la única
