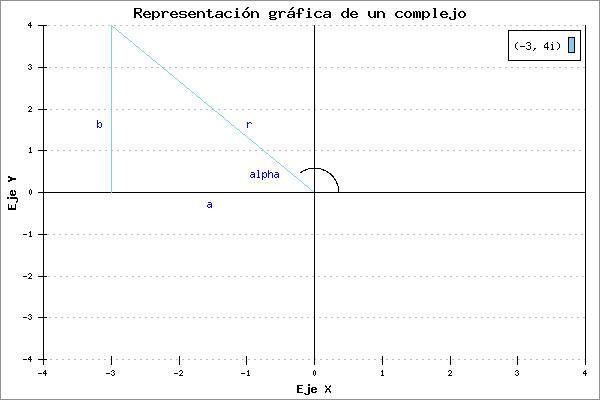
Operaciones de los números complejos
Las operaciones de los complejos z_1, z_2, z_3 \in \mathbb{C}
\begin{cases}z_1=a+b\cdot{i} \\ z_2=c+d\cdot{i} \\ z_3=e+f\cdot{i} \end{cases}
Operación suma
Para definir la suma se han de cumplir las siguientes propiedades
Propiedades de la suma
- z_1+z_2 \in{\mathbb{C}}
- z_1+(z_2+z_3)=(z_1+z_2)+z_3
- \exists\text{ }0 \in \mathbb{C} | z_1+0=0+z_1=z_1
- \exists\text{ }(-z_1) \in \mathbb{C} | z_1+(-z_1)=(-z_1)+z_1=0
- z_1+z_2=z_2+z_1
Como cumple las propiedades anteriores, el par (C, +) tiene estructura de grupo abeliano
Ejemplo de suma
\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1+z_2 \end{cases}
z=((-3)+4\cdot{i})+(5-2\cdot{i})=((-3)+5)+(4-2)\cdot{i}=2+2\cdot{i}
Entonces tenemos que:
z=z_1+z_2=2+2\cdot{i}
Operación resta
La resta es un caso especial de la suma, para realizarla sólo hay que usar la suma del opuesto de sus partes reales y la suma de los opuestos de las partes imaginarias
Ejemplo de resta
\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1-z_2 \end{cases}
z=((-3)+4\cdot{i})-(5-2\cdot{i})=((-3)-5)+(4+2)\cdot{i}=(-8)+6\cdot{i}
Entonces tenemos que:
z=z_1-z_2=(-8)+6\cdot{i}
Operación multiplicación
Para definir la multiplicación se han de cumplir las siguientes propiedades
Propiedades de la multiplicación
- z_1\cdot{z_2} \in{\mathbb{C}}
- z_1\cdot(z_2\cdot{z_3})=(z_1\cdot{z_2})\cdot{z_3}
- \exists\text{ }1 \in \mathbb{C} | z_1\cdot{1}=1\cdot{z_1}=z_1
- \forall\text{ }(z_1) \in \mathbb{C} (z_1\ne{0}), \exists\text{ }{z_1}^-1 \in \mathbb{C} | z_1\cdot{z_1}^-1={z_1}^-1\cdot{z_1}=1
- z_1\cdot{z_2}=z_2\cdot{z_1}
Como cumple las propiedades anteriores, el par (\mathbb{C}-\{0\}, \cdot) tiene estructura de grupo abeliano
Ejemplo de multiplicación
\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1\cdot z_2 \end{cases}
z=((-3)+4\cdot{i})\cdot(5-2\cdot{i})=((-3)\cdot{5})+((-3)\cdot(-2)\cdot{i}))+(4\cdot{i}\cdot{5})+(4\cdot{i}+(-2)\cdot{i})=(-15)+6\cdot{i}+20\cdot{i}-8\cdot{i^2}=(-15)+26\cdot{i}-8\cdot{i^2}=(-15)+8+26\cdot{i}=(-7)+26\cdot{i}
En el caso de obtener un valor imaginario al cuadrado (i^2), tomaremos ese valor como su opuesto real. En el ejemplo nos aparecía (-8)\cdot{i}, tomaremos 8 como número real que se sumará a su parte real
Entonces tenemos que:
z=z_1\cdot{z_2}=(-7)+26\cdot{i}
Operación división
La división es un caso especial de la multiplicación, para realizarla sólo multiplicar el numerador y el denominador por el conjugado del denominador
El conjugado se obtiene de cambiar el signo de la parte imaginaria del denominador
Ejemplo de división
\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z={z_1 \over z_2} \end{cases}
z={((-3)+4\cdot{i})\over(5-2\cdot{i})}={((-3)+4\cdot{i})\over(5-2\cdot{i})}\cdot{(5+2\cdot{i})\over(5+2\cdot{i})}=
{(((-3)\cdot{5})+((-3)\cdot{2}\cdot{i})+(4\cdot{i}\cdot{5})+(4\cdot{i}\cdot{2}\cdot{i}))\over((5\cdot{5})+(5\cdot{2}\cdot{i})+((-2)\cdot{i}\cdot{5})+((-2)\cdot{i}\cdot{2}\cdot{i}))}=
{(-15)+(-6)\cdot{i}+20\cdot{i}+(8\cdot{i^2})\over{25}+10\cdot{i}+(-10)\cdot{i}+(-4)\cdot{i^2}}={(-15)+14\cdot{i}+(8\cdot{i^2})\over{25}+(-4)\cdot{i^2}}=
{(-15)-8+14\cdot{i}\over{25}+4}={(-23)+14\cdot{i}\over{29}}={(-23)\over{29}}+{14\cdot{i}\over{29}}
Entonces tenemos que:
z={z_1 \over z_2}={(-23)\over{29}}+{14\cdot{i}\over{29}}
Operación suma y producto
Además suma y producto comparten la siguiente propiedad
Propiedad de la suma y el producto
- z_1\cdot(z_2+z_3)=z_1\cdot{z_2}+z_1\cdot{z_3}
Como cumple la propiedad anterior, la terna (\mathbb{C}, +, \cdot) tiene estructura de cuerpo conmutativo
Ejemplo de suma y multiplicación
\begin{cases}z_1=(-3)+4\cdot{i} \\ z_2=5-2\cdot{i} \\ z=z_1\cdot(z_2+z_3) \end{cases}
z=((-3)+4\cdot{i})\cdot((5-2\cdot{i})+(8+3\cdot{i}))=((-3)+4\cdot{i})\cdot(5-2\cdot{i}))+((-3)+4\cdot{i})\cdot(8+3\cdot{i}))=((-3)\cdot{5})+((-3)\cdot(-2)\cdot{i})+(4\cdot{i}\cdot{5})+(4\cdot{i}+(-2)\cdot{i})+((-3)\cdot{8})+((-3)\cdot{3}\cdot{i})+(4\cdot{i}\cdot{8})+(4\cdot{i}\cdot{3}\cdot{i})=((-15)+6\cdot{i}+20\cdot{i}-8\cdot{i^2})+((-24)-9\cdot{i}+32\cdot{i}+12\cdot{i^2})=(-15)-24+6\cdot{i}+20\cdot{i}-9\cdot{i}+32\cdot{i}-8\cdot{i^2}+12\cdot{i^2}=(-39)+49\cdot{i}+4\cdot{i^2}=(-39)-4+49\cdot{i}=(-43)+49\cdot{i}
Entonces tenemos que:
z=z_1\cdot(z_2+z_3)=(-43)+49\cdot{i}