Encaminamiento

El encaminamiento, enrutamiento o ruteo, es la función de buscar un camino entre todos los posibles en una red de paquetes cuyas topologías poseen una gran conectividad

Dado que se trata de encontrar la mejor ruta posible y en consecuencia cuál es la métrica que se debe utilizar para medirla

La red debe encontrar una ruta mediante:

• Eficiencia
• Flexibilidad

Los conmutadores de la red se organizan en una estructura en árbol

El encaminamiento estático utiliza la misma aproximación todo el tiempo

El encaminamiento dinámico permite los cambios en el encaminamiento dependiendo del tráfico

Utiliza una estructura de relación de igual a igual para los nodos

Criterios de encaminamiento

Encaminamiento alternativo

Las posibles rutas entre dos centrales finales se encuentran predefinidas

Es responsabilidad del conmutador origen seleccionar el camino adecuado para cada llamada

Cada conmutador dispone de un conjunto de rutas prefijadas, en orden de preferencia

Un conjunto diferente de rutas preplanificadas en instantes distintos de tiempo

Dos tipos:

• Alternativo fijo
  Sólo una secuencia de encaminamiento para cada pareja origen-destino
• Alternativo dinámico
  Conjunto diferente de rutas preplanificadas en instantes distintos de tiempo

Encaminamiento en redes de conmutación de paquetes

Uno de los aspectos más complejos y cruciales del diseño de redes de conmutación de paquetes es el relativo al encaminamiento

Características necesarias:

• Exactitud
• Simplicidad
• Robustez
• Estabilidad
• Imparcialidad
• Optimización
• Eficiencia

Criterios de rendimiento

Se utiliza para la elección de una ruta

Dos técnicas fundamentales:

• Elegir el camino con menor número de saltos: minimiza el consumo de recursos de la red
• Una generalización del anterior es el criterio del mínimo coste
  • En caso de distintos costos por enlaces, se tomará aquel camino que sea el del mínimo coste
  • Si cada nodo tiene igual coste se puede generalizar este criterio buscando el camino de menor número de saltos

Instante y lugar de decisión

• Instante
  • Paquete o datagrama
    Si cambian los costos, el paquete siguiente puede seguir una ruta diferente, de nuevo determinada por cada nodo a lo largo del camino
  • Circuito virtual
    Cada nodo recuerda la decisión de encaminamiento tomada cuando se estableció el circuito virtual, de modo que se limita a transmitir los paquetes sin tomar decisiones nuevas
• Lugar
  • Encaminamiento distribuido
    • Se lleva a cabo por cada nodo
    • Es el más robusto
  • Encaminamiento centralizado
  • Encaminamiento desde el origen

Fuente de información de la red y tiempo de actualización

Las decisiones de encaminamiento se suelen tomar en base al conocimiento de la red, la carga y el coste de los enlaces (pero no siempre como por ejemplo con inundaciones y encaminamiento aleatorio)

• Encaminamiento distribuido
  • Los nodos hacen uso de información local (coste asociado a cada enlace de salida)
  • Pueden utilizar información de los nodos adyacentes (congestión entre ellos)
  • Pueden obtener información de todos los nodos de una potencial ruta de interés
• Encaminamiento central
  • Recopilar información de todos los nodos
• Tiempo de actualización
  • Cuando los nodos tienen información actualizada de la red
  • Para una estrategia de encaminamiento estático, la información no se actualiza nunca
  • Para una técnica adaptable, la actualización se lleva a cabo periódicamente

Estrategias de encaminamiento ARPANET

Primera generación: 1969

• Algoritmo adaptable distribuido
• Estimación de los retardos como criterio de funcionamiento
• Algoritmo de Bellman-Ford
• Cada nodo intercambia su vector de retardo con todos sus vecinos
• Tabla de encaminamiento actualizada basándose en la información de entrada
• No tiene en cuenta la velocidad de la línea, sino la longitud de la cola
• La longitud de la cola no es una buena medida del retardo
• Responde lentamente a la congestión

Segunda generación: 1979

• Se hace uso del retardo como criterio de rendimiento
• El retardo se mide directamente
• Algoritmo de Dijkstra
• Es bueno ante cargas bajas o moderadas
• Ante cargas altas, existe poca correlación entre los retardos indicados y los experimentados

Tercera generación: 1987

• Cambian las estimaciones del coste del enlace
• Medida del retardo medio en los últimos 10 segundos
• Se normaliza en base al valor actual y a los resultados previos

Estrategias de encaminamiento

Encaminamiento estático

Una única ruta permanente para cada par de nodos origen-destino en la red

Se determinar las rutas utilizando cualquiera de los algoritmos de encaminamiento de mínimo coste

Las rutas son fijas, al menos mientras lo sea la topología de la red

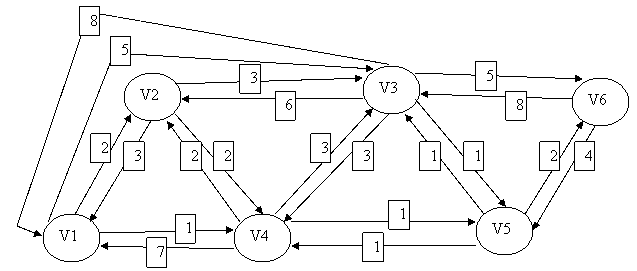
Ejemplo de encaminamiento estático

Matriz de encaminamiento central

{\tiny\text{Nodo destino}}\overset{\text{Nodo origen}}{\begin{pmatrix}& 1& 2& 3& 4& 5& 6 \\ 1& & 1& 5& 2& 4& 5 \\ 2& 2& & 5& 2& 4& 5 \\ 3& 4& 3& & 5& 3& 5 \\ 4& 4& 4& 5& & 4& 5 \\ 5& 4& 4& 5& 5& & 5 \\ 6& 4& 4& 5& 5& 6 \\ \end{pmatrix}}

Tabla del nodo 1
Destino	Nodo siguiente
2	2
3	4
4	4
5	4
6	4

Tabla del nodo 2
Destino	Nodo siguiente
1	1
3	3
4	4
5	4
6	4

Tabla del nodo 3
Destino	Nodo siguiente
1	5
2	5
4	5
5	5
6	5

Tabla del nodo 4
Destino	Nodo siguiente
1	2
2	2
3	5
5	5
6	5

Tabla del nodo 5
Destino	Nodo siguiente
1	4
2	2
3	3
4	4
6	6

Tabla del nodo 6
Destino	Nodo siguiente
1	5
2	5
3	5
4	5
5	5

Inundaciones

No precisa de ninguna información sobre la red. Un nodo origen envía un paquete a todos sus nodos vecinos. Los nodos vecinos, a su vez, lo transmiten sobre todos los enlaces de salida excepto por el que llegó. Finalmente, llegará un número de copias al destino

Cada paquete contiene un identificador único, por lo que se pueden descartar los duplicados. De esta forma, una técnica sería que los nodos puedan recordar la identidad de los paquetes que han retransmitido con anterioridad, de manera que se evitan las cargas de la red

Otra técnica más sencilla es que se pueda incluir un campo de cuenta de saltos en cada paquete, un tiempo de vida donde cada vez que un nodo transmite un paquete, decrementa la cuenta en 1, de modo que cuando el contador alcanza el valor cero de elimina el paquete de la red

Propiedades

• Se prueban todos los posibles caminos entre los nodos origen y destino. Lo que nos ofrece robustez
  Ejemplo: el envío de un mensaje de alta prioridad para garantizar la recepción del paquete
• Al menos una copia del paquete a recibir en el destino habrá usado una ruta de menor número de saltos. Podría emplearse inicialmente para establecer la ruta para un circuito virtual
• Se visitan todos los nodos. Puede resultar útil para llevar a cabo la propagación de información relevante para todos los nodos (por ejemplo, una tabla de encaminamiento central)

Ejemplo de inundación

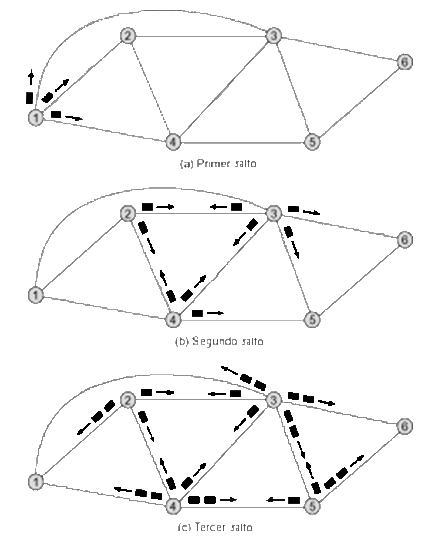
Encaminamiento aleatorio

Un nodo selecciona un único camino de salida para retransmitir un paquete entrante. La selección se puede hacer de forma aleatoria o alternada

Una mejoría es que se pueda seleccionar la ruta de salida de acuerdo con el cálculo de probabilidades

No necesita el uso de información sobre la red. La ruta no corresponderá en general con la de mínimo coste ni con la de menor número de saltos. Tiene menos tráfico que la de inundaciones pero es igualmente sencilla y robusta.Un nodo selecciona un único camino de salida para retransmitir un paquete entrante. La selección se puede hacer de forma aleatoria o alternada

Una mejoría es que se pueda seleccionar la ruta de salida de acuerdo con el cálculo de probabilidades

No necesita el uso de información sobre la red. La ruta no corresponderá en general con la de mínimo coste ni con la de menor número de saltos. Tiene menos tráfico que la de inundaciones pero es igualmente sencilla y robusta

Encaminamiento adaptable

Prácticamente en todas las redes de conmutación de paquetes se utiliza algún tipo de técnica de encaminamiento adaptable

Las decisiones de encaminamiento cambian en la medida que lo hacen las condiciones de la red:

• Fallos
• Congestión

Requiere información acerca del estado de la red presentando desventajas:

• Las decisiones son más complejas: mayor coste de procesamiento en los nodos de la red
• Es necesario que los nodos intercambien información acerca del estado y del tráfico de la red: mayor tráfico y degradación de las prestaciones de la red
• La reacción demasiado rápida puede provocar oscilación o ser demasiado lenta para ser relevante

Ventajas del encaminamiento adaptable

• Mejora de las prestaciones
• Resulta de ayuda en el control de la congestión
• Sistema complejo: Puede que no se cumplan los beneficios teóricos

Clasificación

Clasificación realizada de acuerdo con la fuente de información

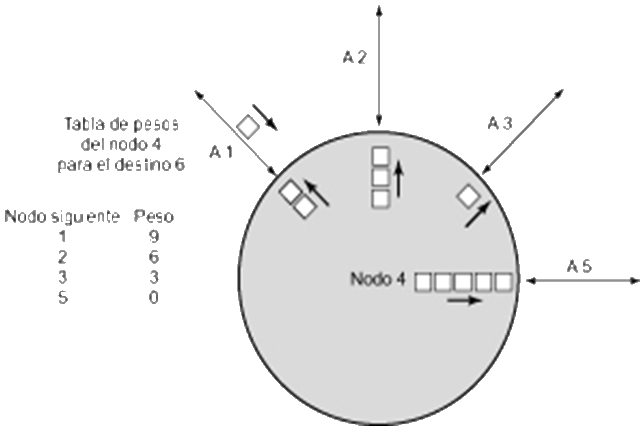
• Local (aislada)
  • Encaminar el paquete hasta el enlace de salida con la cola más corta
  • Puede incluir un peso para cada destino. Se utilizan raramente, puesto que no explotan con facilidad la información disponible
• Nodos adyacentes
• Todos los nodos

Ejemplo de encaminamiento adaptable aislado

Petri

Una Red de Petri es una representación matemática o gráfica de un sistema a eventos discretos en el cual se puede describir la topología de un sistema distribuido, paralelo o concurrente

La red de Petri esencial fue definida en los años 60 por Carl Adam Petri

Son una generalización de la teoría de autómatas que permite expresar un sistema de eventos concurrentes

Una red de Petri está formada por lugares, transiciones, arcos dirigidos y marcas o fichas que ocupan posiciones dentro de los lugares

Las reglas son: Los arcos conectan un lugar a una transición así como una transición a un lugar

No puede haber arcos entre lugares ni entre transiciones

Los lugares contienen un número finito o infinito contable de marcas

Las transiciones se disparan, es decir consumen marcas de una posición de inicio y producen marcas en una posición de llegada. Una transición está habilitada si tiene marcas en todas sus posiciones de entrada

En su forma más básica, las marcas que circulan en una red de Petri son todas idénticas

Se puede definir una variante de las redes de Petri en las cuales las marcas pueden tener un color (una información que las distingue), un tiempo de activación y una jerarquía en la red

La mayoría de los problemas sobre redes de Petri son decidibles, tales como el carácter acotado y la cobertura

Para resolverlos se utiliza un árbol de Karp-Miller. Se sabe que el problema de alcance es decidible, al menos en un tiempo exponencial

Utilidad en el análisis cualitativo

Para realizar el análisis cualitativo de una red se pueden utilizar las Redes de Petri, ya que son grafos bipartidos

Según cómo analicemos la red de Petri podremos encontrarnos con:

• Análisis estructural (dependen de la estructura)
  Tienen las siguientes propiedades:
  • Repetitiva
    Existe una secuencia de disparos, incluyendo todas las transiciones, que si se pueden disparar dejan al sistema igual que al principio \Longleftrightarrow Existe un vector anulador derecho de la matriz de incidencia con todos sus términos enteros positivos
  • Conservativa
    Existe una combinación de pesos enteros positivos que si se aplican a los lugares, la suma del marcado de todos los lugares ponderados por sus pesos es invariante (siempre igual) \Longleftrightarrow Existe un vector anulador izquierdo de la matriz de incidencia con todos sus términos enteros positivos
  • Cerrojos
    Lugar o conjunto de lugares en los que las marcas que contienen no pueden disminuir, debido a que las transiciones de salida de esos lugares son también de entrada, con mayor peso total en los arcos de entrada (a los lugares de la trampa) que los de salida. Una fila o suma de filas con valores negativos o cero en la matriz de incidencia, contendrá un cerrojo
  • Trampas
    Lugar o conjunto de lugares en los que las marcas que contienen no pueden aumentar, debido a que las transiciones de entrada a esos lugares son también de salida, con mayor peso total en los arcos de salida (de los lugares de la trampa) que los de entrada. Una fila o suma de filas con valores positivos o cero en la matriz de incidencia, contendrá una trampa
  • Cerrojo / Trampa
    Es a la vez cerrojo y trampa. Una fila o suma de filas con todos los valores cero en la matriz de incidencia, contendrá un cerrojo / trampa
• Análisis dinámico (dependen del marcado inicial)
  Tienen las siguientes propiedades:
  • Cíclica
    Dado un estado inicial, desde cualquier estado accesible siempre se puede volver al estado inicial
  • Viva
    Dado un estado inicial, desde cualquier estado accesible nunca habrá una transición que ya no se pueda disparar más adelante
  • Limitada
    Todos los lugares tienen una cota superior finita

Método Simplex

Se puede emplear el método Simplex para la resolución de problemas consistentes en maximizar o minimizar una función lineal de variables, con restricciones en forma de igualdades o desigualdades de funciones lineales de dichas variables, y con todas las variables acotadas superior o inferiormente

Aplicando los siguientes pasos:

1. Planteamiento del problema en forma estándar
2. Aplicación del algoritmo del Simplex
3. Determinación de la solución obtenida

Paso 1: Planteamiento del problema en forma estándar

1. Se debe poner la función como «minimizar»
2. Si es necesario, se realizan cambios de variable para que todas las variables tengan 0 como cota inferior (X_i\geq 0, \forall i)
3. Las restricciones se ponen con el término constante positivo
4. Se convierten las desigualdades de las restricciones en igualdades añadiendo las variables de holgura
5. Se añaden variables artificiales en las restricciones que no tienen una variable en la base, y se añade a la función objetivo la suma de esas variables artificiales multiplicadas por M (que se considera con un valor altísimo)
6. Se rellena la tabla para aplicar el algoritmo del Simplex. Su estructura es la siguiente:
   

   	X_1 \cdots X_n
   X básicas	a	b
   	c-z

   X_1 \cdots X_n es la alineación de las variables originales, las variables de holgura y las variables artificiales

   a son los términos de dichas variables en las restricciones

   b son los elementos constantes de dichas restricciones (al otro lado de las variables en las igualdades)

   c - z son los costes marginales, en los que c son los coeficientes de la función objetivo, y z_i=c_{b_1}\cdot a_{1 j}+\cdots+c_{b_m}\cdot a_{m i}, siendo m el número de restricciones (de elementos en la base), y donde c_{b_j} representa el coeficiente de la función objetivo correspondiente a la variable j-ésima de las que componen la base. Notar que c - z = 0 siempre para las variables de la base

Paso 2: Aplicación del algoritmo del Simplex

1. Elección de la columna de pivote
   Se busca el menor elemento de la fila c - z, c\cdot k - z\cdot k de entre los que son negativos y tienen algún elemento positivo en la columna a_k. Si no hay ninguno se termina el algoritmo
2. Elección de la fila de pivote
   Entre los elementos positivos de a_k se busca el que tenga mínimo coeficiente: \frac{b_i}{a_{i k}}, lo llamaremos a_{r k}, y ése será el elemento sobre el que pivotaremos. Si hay varios con el mismo coeficiente se escoge uno cualquiera
3. Eliminación gaussiana
   Se pivota sobre a_{r k}, es decir, se convierte a_k en un vector de la base canónica. Para ello primero se dividen todos los términos de la fila r de a entre a_{r k}, con lo que el nuevo a_{r k} tendrá valor 1 (al dividirse entre sí mismo). Después se anulan los demás elementos de a_k mediante eliminación gaussiana (a cada fila i, con i \not= r, se le suma la nueva fila r multiplicada por X_k). Con ello la variable -a_{i k} habrá entrado en la base (y estará situada en la fila r)
4. Repetir
   Hasta que (c_j - z_j\geq 0, \forall j) \cup (a_k < 0, \forall k\longrightarrow c_k - z_k < 0)

Paso 3: Determinación de la solución obtenida

Si el problema tiene variables artificiales y alguna de ellas presenta valor distinto de cero en la solución final, entonces el problema planteado no tiene solución (no es factible). En caso contrario pasar a los casos siguientes:

1. Si (c_j - z_j\geq 0, \forall j) \cap (c_k - z_ k > 0) para las variables no básicas entonces tenemos solución única
2. Si (c_j - z_j\geq 0, \forall j) \cap (c_k - z_k = 0) para alguna variable no básica entonces tenemos solución múltiple
3. Si \exists (c_k - z_k < 0) (todos ellos han de cumplir que a_k < 0) entonces tenemos una solución no acotada

Ejemplo de problema de Método Simplex

En el gráfico se muestra la representación de una red de comunicación en la que en cada tramo representa la capacidad máxima de transferencia por unidad de tiempo

Se pide:

1. Plantea un PPL (problema de programación lineal) cuya solución nos dé la máxima capacidad de transferencia entre A y B y entre C y D (la suma de ambas)
2. Resolver el PPL (problema de programación lineal), indicando el tipo de solución que es, su valor, si existe solución, y explicarla

Parte a)

Entre A y B hay 3 caminos que son:

\begin{cases} X_1 \text{ por el camino }A-B \\ X_2 \text{ por el camino }A-D-B \\ X_3 \text{ por el camino }A-D-C-B \end{cases}

Entre C y D hay 3 caminos que son:

\begin{cases} X_4 \text{ por el camino }C-B-A-D \\ X_5 \text{ por el camino }C-B-D \\ X_6 \text{ por el camino }C-D \end{cases}

Por tanto la función a optimizar es:

(X_1+X_2+X_3)+(X_4+X_5+X_6)

Con las restricciones:

\begin{cases} X_1+X_4 \leq 2 \\ X_2+X_3+X_4 \leq 1 \\ X_3+X_4+X_5 \leq 2 \\ X_2+X_5 \leq 2 \\ X_3+X_6 \leq 1 \end{cases}

Con X_1, X_2, X_3, X_4, X_5, X_6 > 0

Parte b)

Maximizar (X_1+X_2+X_3)+(X_4+X_5+X_6)
Minimizar (-X_1-X_2-X_3)+(-X_4-X_5-X_6)

\begin{cases} X_1+X_4+h_1 = 2 \\ X_2+X_3+X_4+h_2 = 1 \\ X_3+X_4+X_5+h_3 = 2 \\ X_2+X_5+h_4 = 2 \\ X_3+X_6+h_5 = 1 \end{cases}

Valores c - z:
columna \tiny X_1 = -1 - ( (-1) \cdot 1 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny X_2 = -1 - ( (-1) \cdot 0 + 0 \cdot 1 + 0 \cdot 0 + 0 \cdot 1 + (-1) \cdot 0 ) = -1
columna \tiny X_3 = -1 - ( (-1) \cdot 0 + 0 \cdot 1 + 0 \cdot 1 + 0 \cdot 0 + (-1) \cdot 1 ) = 0
columna \tiny X_4 = -1 - ( (-1) \cdot 1 + 0 \cdot 1 + 0 \cdot 1 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny X_5 = -1 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 1 + 0 \cdot 1 + (-1) \cdot 0 ) = -1
columna \tiny X_6 = -1 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 1 ) = 0
columna \tiny h_1 = 0 - ( (-1) \cdot 1 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 0 ) = 1
columna \tiny h_2 = 0 - ( (-1) \cdot 0 + 0 \cdot 1+ 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny h3 = 0 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 1 + 0 \cdot 0 + (-1) \cdot 0 ) = 0
columna \tiny h4 = 0 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 1 + (-1) \cdot 0 ) = 0
columna \tiny h5 = 0 - ( (-1) \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + 0 \cdot 0 + (-1) \cdot 1 ) = 1

\tiny{\begin{pmatrix}& -1\hspace{1 mm} X_1& -1\hspace{1 mm} X_2& -1\hspace{1 mm} X_3& -1\hspace{1 mm} X_4& -1\hspace{1 mm} X_5& -1\hspace{1 mm} X_6& 0\hspace{1 mm} h_1& 0\hspace{1 mm} h_2& 0\hspace{1 mm} h_3& 0\hspace{1 mm} h_4& 0\hspace{1 mm} h_5& \cr -1\hspace{1 mm} X_1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 2 \cr 0\hspace{1 mm} h_2& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 0& 1 \cr 0\hspace{1 mm} h_3& 0& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 2 \cr 0\hspace{1 mm} h_4& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 0& 2 \cr -1\hspace{1 mm} X_6& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1 \cr & 0& -1& 0& 0& -1& 0& 1& 0& 0& 0& 1&\end{pmatrix}}

Elegimos como pivote la fila 2, columna 2. Por tanto en este caso \frac{b_i}{a_{i k}} será \frac{1}{1}=1

\tiny{\begin{pmatrix}& -1\hspace{1 mm} X_1& -1\hspace{1 mm} X_2& -1\hspace{1 mm} X_3& -1\hspace{1 mm} X_4& -1\hspace{1 mm} X_5& -1\hspace{1 mm} X_6& 0\hspace{1 mm} h_1& 0\hspace{1 mm} h_2& 0\hspace{1 mm} h_3& 0\hspace{1 mm} h_4& 0\hspace{1 mm} h_5& \cr -1\hspace{1 mm} X_1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 2 \cr 0\hspace{1 mm} X_2& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 0& 1 \cr 0\hspace{1 mm} h_3& 0& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 2 \cr 0\hspace{1 mm} h_4& 0& 0& -1& -1& 1& 0& 0& -1& 0& 1& 0& 1 \cr -1\hspace{1 mm} X_6& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1 \cr & 0& 0& 1& 1& -1& 0& 1& 1& 0& 0& -1& 1\end{pmatrix}}

Elegimos como pivote la fila 4, columna 5. Por tanto en este caso \frac{b_i}{a_{i k}} será \frac{1}{1}=1

\tiny{\begin{pmatrix}& -1\hspace{1 mm} X_1& -1\hspace{1 mm} X_2& -1\hspace{1 mm} X_3& -1\hspace{1 mm} X_4& -1\hspace{1 mm} X_5& -1\hspace{1 mm} X_6& 0\hspace{1 mm} h_1& 0\hspace{1 mm} h_2& 0\hspace{1 mm} h_3& 0\hspace{1 mm} h_4& 0\hspace{1 mm} h_5& \cr -1\hspace{1 mm} X_1& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 2 \cr 0\hspace{1 mm} h_2& 0& 1& 1& 1& 0& 0& 0& 1& 0& 0& 0& 1 \cr 0\hspace{1 mm} h_3& 0& 0& 2& 2& 0& 0& 0& 1& 1& -1& 0& 1 \cr 0\hspace{1 mm} X_5& 0& 0& -1& -1& 1& 0& 0& -1& 0& 1& 0& 1 \cr -1\hspace{1 mm} X_6& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 1& 1 \cr & 0& 0& 0& 0& 0& 0& 1& 0& 0& 1& -1& 2\end{pmatrix}}

Como no hay más valores negativos en los c – z, c_k - z_k que podamos pivotar, cesamos el algoritmo y obtenemos el siguiente resultado:

\begin{cases} X_1 = 2 \\ X_2 = 1 \\ X_5 = 1 \\ X_6 = 1 \end{cases}

Por tanto, tenemos que X_3 = 0 y X_4 = 0 para que se cumplan las restricciones. Por lo que tenemos que una posible solución a nuestro problema es:

(X_1+X_2+X_3)+(X_4+X_5+X_6) = 5

La solución es múltiple, por tanto, esta solución no es la única

Algoritmo Bellman-Ford

El algoritmo Bellman-Ford resuelve los problemas en los que hay que encontrar los caminos más cortos desde un nodo origen dado con la condición de que éstos contengan a lo sumo un enlace

Encontrar los caminos más cortos con la condición de que contengan dos enlaces como máximo

Y así sucesivamente hasta el número máximo de caminos más cortos

Donde:

• s = nodo origen
• w(i, j) = coste del enlace desde el nodo i al nodo j:
  • w(i, i) = 0
  • w(i, j) = \infty si los dos nodos no se encuentran directamente conectados
  • w(i, j) \geq 0 si los dos nodos están directamente conectados
• h = número máximo de enlaces en un camino en el paso actual del algoritmo
• L_h(n) = coste del camino de mínimo coste desde el nodo s hasta el nodo n con la condición de que no haya más de h enlaces

Para su resolución se puede emplear el método del algoritmo Bellman-Ford, que consiste en aplicar los siguientes pasos:

1. Inicialización
2. Actualización

Paso 1: Inicialización

L_0(n) = \infty, \forall n \not= s
L_h(n) = 0, \forall h

Paso 2: Actualización

1. Para cada sucesivo h \geq 0, \forall n \not= s calcular:
   L_{h+1}(s)=\min_j{[L_h(j)+w(j, n)]}
2. Conectar n con el nodo predecesor j de mínimo coste
3. Eliminar todas las conexiones de n con un nodo predecesor diferente obtenido en una iteración anterior
4. El camino de s a n finaliza con el enlace de j a n

Anotaciones al algoritmo Bellman-Ford

Para la iteración del paso 2 con h = K, y para cada nodo de destino n, el algoritmo compara las rutas potenciales de longitud K + 1 desde s hasta n con el camino existente al final de la iteración anterior

Si el camino más corto previo tiene un coste inferior, se guarda

En caso contrario, se define un nuevo camino

Ejemplo del algoritmo Bellman-Ford

En el gráfico se muestra la representación de una red de comunicación en la que en cada tramo representa la capacidad máxima de transferencia por unidad de tiempo

Se pide:

Llegar del nodo V1 al nodo V6

h	L_h(2)	Ruta	L_h(3)	Ruta	L_h(4)	Ruta	L_h(5)	Ruta	L_h(6)	Ruta
0	\infty	–	\infty	–	\infty	–	\infty	–	\infty	–
1	2	1-2	5	1-3	1	1-4	\infty	–	\infty	–
2	2	1-2	4	1-4-3	1	1-4	2	1-4-5	10	1-3-6
3	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5-6
4	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5-6

Según el algoritmo Bellman-Ford deberemos seguir los nodos V1-V4-V5-V6, por ser los que menor coste nos ocasionan

Algoritmo Dijkstra

El algoritmo Dijkstra resuelve los problemas en los que hay que encontrar las rutas más cortas entre un nodo origen dado y todos los demás nodos, desarrollando los caminos en orden creciente de longitud

Donde:

• N = conjunto de nodos en la red
• s = nodo origen
• T = lista o conjunto de nodos añadidos o incorporados por el algoritmo
• w(i, j) = coste del enlace desde el nodo i al nodo j:
  • w(i, i) = 0
  • w(i, j) = \infty si los dos nodos no se encuentran directamente conectados
  • w(i, j) \geq 0 si los dos nodos están directamente conectados
• L_h(n) = coste en curso obtenido por el algoritmo para el camino de mínimo coste del nodo s al nodo n

Para su resolución se puede emplear el método del algoritmo Dijkstra, que consiste en aplicar los siguientes pasos:

1. Inicialización
2. Obtención del siguiente nodo
3. Actualización de los caminos de mínimo coste

Paso 1: Inicialización

T = {s} el conjunto de nodos incorporado sólo consta del nodo origen

L(n) = w(s, n), \forall n \not= s

El coste inicial de las rutas a los nodos vecinos es el asociado a los enlaces

Paso 2: Obtención del siguiente nodo

1. Se busca el nodo vecino que no esté en T con el camino de menor coste
2. Se incorpora el nodo en T
3. Se incorpora el enlace desde ese nodo hasta un nodo de T que forma parte del camino

Paso 3: Actualización de los caminos de mínimo coste

Se aplica la siguiente fórmula:

L(n) = \min{[L(n), L(x) + w(x, n)]}, \forall n \not\in T

El algoritmo concluye cuando todos los nodos han sido añadidos a T

Anotaciones al algoritmo Dijkstra

Al final, el valor L(x) asociado a cada nodo x es el coste (longitud) de la ruta de mínimo coste de s a x

T define la ruta de mínimo coste desde s hasta cualquier otro nodo

Cada iteración de los pasos 2 y 3 incorpora un nuevo nodo a T que define el camino de mínimo coste desde s hasta ese nodo, atravesando dicha ruta sólo nodos incluidos en T

Ejemplo del algoritmo Dijkstra

En el gráfico se muestra la representación de una red de comunicación en la que en cada tramo representa la capacidad máxima de transferencia por unidad de tiempo

Se pide:

Llegar del nodo V1 al nodo V6

i	T	L_h(2)	Ruta	L_h(3)	Ruta	L_h(4)	Ruta	L_h(5)	Ruta	L_h(6)	Ruta
1	{1}	2	1-2	5	1-3	1	1-4	\infty	–	\infty	–
2	{1, 4}	2	1-2	4	1-4-3	1	1-4	2	1-4-5	\infty	–
3	{1, 2, 4}	2	1-2	4	1-4-3	1	1-4	2	1-4-5	\infty	–
4	{1, 2, 4, 5}	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5–6
5	{1, 2, 3, 4, 5}	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5–6
6	{1, 2, 3, 4, 5, 6}	2	1-2	3	1-4-5-3	1	1-4	2	1-4-5	4	1-4-5–6

Según el algoritmo Dijkstra deberemos seguir los nodos V1-V4-V5-V6, por ser los que menor coste nos ocasionan